A while ago one of my friends had an idea for a 3D game where you can only see parts of the world at once. Think of a volume, like a cube, within which the world exists and is visible, but outside which there is nothing. The volume exists as a 3D window into the world, so as it moves around in space different parts of the world are revealed to you. Take this horribly-lit screenshot with some terribly-modelled terrain:

On the left you can see the whole world, and on the right you can see the whole world as viewed through three cuboid volumes. You can see the terrain and objects have been sliced around each cuboid, so they are only partially visible. Imagine a puzzle where a key is locked inside a box, and the solution is to move one of these windows so you can see the inside, and then fire a grapple across the void to retrieve it. That’s roughly where we were going with this!
Slicing a Mesh
To achieve what we wanted, we would need to be able to slice any 3D objects that intersect with the edges of the volume. There’s a few steps to get there, and a few things to understand about meshes, so let’s break the problem down and keep it as simple as possible.
Firstly, for simplicity, let’s say the volumes are always cuboids. This means for each volume we need to slice an intersecting mesh up to 4 times. Secondly, we need to understand that all meshes are made up of triangles, which are in-turn made up of three vertices each. The steps we will then follow to slice the mesh are:
1
2
3
4
5
6
7
For each plane:
If the mesh intersects this plane:
For each triangle:
If the triangle is entirely behind the plane, scrap it
If the triangle is entirely in-front of the plane, keep it
If the triangle intersects the plane, slice it
Fill any visible holes at the intersection plane
To check whether the mesh intersects the plane, we can do two things: First, we can do a simple bounding-box check between the plane and a box enclosing the mesh. This is a fast approximate check that allows us to immediately discard anything that’s nowhere near the plane, but doesn’t guarantee that the mesh does intersect the plane. To check that, we’ll need to loop over all of the triangles in the mesh until we find one that intersects. If none intersect, we can skip slicing with this plane.
If the mesh and plane DO intersect, then we’ve got some work to do. For each triangle, we need to determine whether to slice it, and then perform the slice. To determine whether we need to slice it, we can count how many of that triangle’s points are on each side of the plane (using Unity’s handy Plane.GetSide() method). If all points are on the ‘inside’ (the side that the plane normal is pointing), then we can just keep that triangle. If all the points are on the ‘outside’ (opposite the plane normal), then we can throw that triangle away.
Things get a bit more complicated when the triangle’s points lie across both sides of the plane. The simplest case is where only one point is on the ‘inside’, as we just need to find the intersection point of the two connected edges with the plane, and replace the other two vertices with these points (essentially clamping the triangle within the plane).
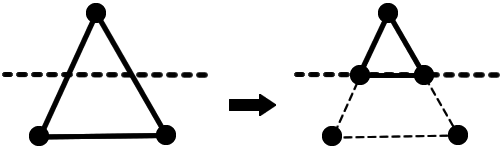
If two points are on the inside, and one on the outside, we need to again find the intersection point of the connected edges with the plane. However, we are now left with four points, which requires us to create two triangles. Still fairly straightforward, you just need to be careful of the winding order of your triangles so you’re not accidentally rendering them back-to-front.
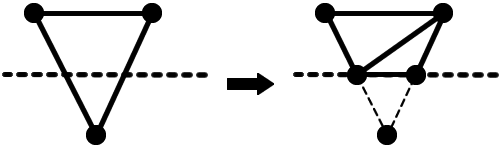
Just repeat that process for every triangle in the mesh and it’ll be sliced! …Well, almost.

Filling in holes
Obviously, this doesn’t look quite right. The mesh here is a jigsaw-piece (lovingly ripped from Banjo-Kazooie), with a wireframe material on it to show you where all the triangles are, and we’ve sliced it using a plane that’s parallel to its front face. If you look around the remaining faces, you can see where we have clamped some triangles and created new ones to slice the mesh along a plane, so that’s a success at least, but you might also have noticed the massive gaping hole where the front face should be. All of the front faces are behind the slicing plane, so they were all thrown away! We’re going to need to more-or-less recreate them from the remaining vertices that we created along the slicing plane. (The back-face is also missing from this screenshot, but that’s because game engines typically ignore back-facing triangles to save time when rendering - They should never be visible anyway!)
An important consideration for this particular mesh is that we are left with a convex shape thanks to the ‘tabs’ and ‘slots’ in the jigsaw piece (note: there is no agreed-upon terminology for the innie and outie bits of a jigsaw piece). For this reason, we can’t just find all of the outer-most points on the intersection plane and connect them with triangles. Instead, we can use a method called ‘advancing-front’ to generate the inside mesh. My implementation is a bit cheap and dirty, and works by creating a triangle between the two neighbouring edges with the smallest signed angle repeatedly until the gap is completely filled. By always connecting the edges with the smallest signed angle, we make sure that no triangles are ever generated outside the convex shape. The topology is pretty ugly, but it does the trick:
And that’s it! All that’s left to do is pass the resulting mesh into the slicing algorithm for the next 3 planes of the volume, stick it into the Unity MeshFilter, and we’re finished. It would also be good in the future to consider the UV coordinates and normals of the resulting vertices, so textures and lighting look correct.
There’s a lot of optimisation that can be done with this kind of algorithm - particularly when using C# to make sure heap allocations are kept to a minimum, and being careful with the vector maths to make sure we’re only doing as much work as absolutely necessary. This is also a great candidate for a Unity Entity Component System to parallelise this for every sliced mesh in the scene.
Unfortunately we could never figure out enough interesting puzzle elements to continue with the game, but I at least found this bit of tech quite interesting!